ECE 140: Linear Circuits¶
Voltage, current, and resistance¶
Please see SL Physics 1#Electric potential for more information on voltage.
Please see SL Physics 1#5.2 - Heating effect of electric currents for more information on current.
Please see SL Physics 1#Resistance for more information on resistance.
Electric charge quantises the charge of electrons and positive ions, and is expressed in coulombs (C).
Objects with charge generate electric fields, thus granting potential energy that is released upon proximity to another charge.
Warning
Voltage and current are capitalised in direct current only (, ). In general use, their lowercase forms should be used instead (i$).
Voltage is related to the change in energy () over the change in charge (), or alternatively through Ohm's law:
Current represents the rate of flow of charge in amps (A). Conventional current moves opposite electron flow because old scientists couldn't figure it out properly.
Power¶
Power represents the rate of doing work, in unit watts (, \pu{J/s})
It is also directly related to voltage and current:
Much like relative velocity, power is directional and relative, with a positive sign indicating the direction of conventional current.
In a closed system, conservation of energy applies:
The ground is the "absolute zero" voltage with a maximum potential difference. It is also known as the "reference voltage".
Independent energy sources¶
Definition
- A ground is the reference point that all potential differences are relative to.
A generic voltage source provides a known potential difference between its two terminals that is defined by the source. The resultant current can be calculated.
(Source: Wikimedia Commons)
A generic current source provides a known amperage between its two terminals that is defined by the source. The resultant voltage can be calculated.
(Source: Wikimedia Commons)
Tip
A current in the positive direction indicates that the source is releasing power (is a source). Otherwise, it is consuming power (is a load).
Dependent energy sources¶
A dependent <T: voltage | current> source has a T dependent on the voltage or current elsewhere in the circuit. is a function that is likely but not guaranteed to be linear.
(Source: Wikimedia Commons)
(Source: Wikimedia Commons)
Applications¶
A cathode ray tube produces an electron beam of variable intensity depending on the input signal. Electrons are deflected by the screen to produce imagery.
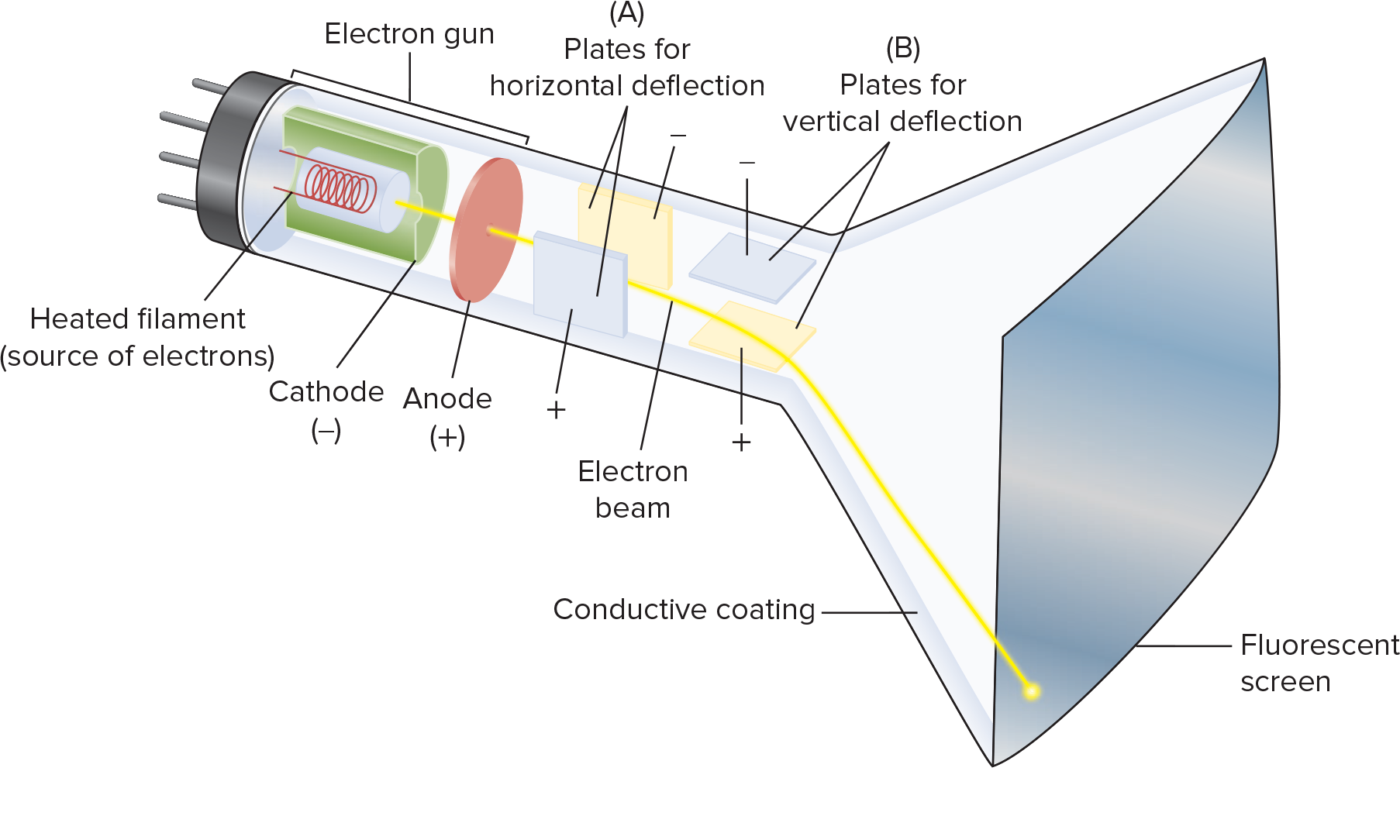
Resistance¶
A resistor always absorbs power, so must be oriented such that current goes into the positive sign.
According to Ohm's law, the voltage, current, and resistance are related:
The conductance of a resistor is the inverse of its resistance, and is expressed in siemens ()
Therefore, power can be expressed by manipulating the equations:
Kirchhoff's laws¶
Definition
- A node is any point in the circuit to which 3+ elements are directly connected (i.e., all junctions).
- A supernode is any connected group in the circuit to which 3+ elements are directly connected.
- A loop is any closed path of elements.
Kirchhoff's current law states that the sum of all current entering a node must be zero, where positive indicates current entrance.
Kirchoff's voltage law states that the sum of all voltage in a closed loop must be zero.
Nodal analysis¶
Nodal analysis uses the voltages at the nodes instead of elements to calculate things in a three-step process:
- Determine a reference node with and stick a ground out of that node.
- Use KCL and Ohm's law on non-reference nodes to get their currents in terms of the reference node.
- Solve the system of equations with the formula below.
On either side of a resistor, the current flowing that entire segment can be determined via the following formula:
Mesh analysis¶
Definition
- A mesh is a loop with no inner loops.
- A supermesh is a combination of multiple meshes that share a common current source.
Mesh / loop analysis is used to determine unknown currents, using KVL instead of KCL to create a system of equations.
- Assign mesh currents to each loop.
- Use KVL and Ohm's law to get voltages in terms of mesh currents.
- Solve the system of equations.
It may be easier to delete the branch of the current source in supermeshes, treating the region as one mesh with multiple mesh currents.
Linearity¶
Circuits are linear if and only if their voltages, resistances, and currents can be expressed in terms of linear transformations of one another. They contain only linear loads, linear dependent sources, and independent souces.
Example
Halving voltage must halve current (or at least halve it relative to a base current / voltage).
Superposition¶
In linear circuits, the superposition principle states that the voltage/current through an element is equal to the sum of the voltages/currents from each independent source alone.
To do so, each unused independent source should be replaced with a short circuit (voltage) or an open circuit (current).
Source transformation¶
In linear circuits, a voltage source in series with a resistor can be replaced by a current source in parallel to that resistor (or vice versa), so long as Ohm's law is followed for the replacement:
The arrow of the current source must point in the positive direction of the voltage source. This can also be used with dependent sources.
Thevenin's theorem¶
Any part of a circuit including an independent source can be replaced with exactly one voltage source and a resistor in series. Two circuits are Thevenin equivalent if their are equal in .
If there are no dependent sources, all independent sources should be removed to determine the resistance across points :
Otherwise, and should be found by repeating these steps:
- Cut off the load (open if finding voltage, short if finding current)
- If dependent sources depend on elements inside the load branch, zero them
- Use analysis to determine the desired quantity
Across the load:
Warning
A negative resistance indicates that the load supplies power.
Maximum power transfer¶
To maximise the power transferred from the circuit to the load, should be equal to .
Operational amplifiers¶
The entire op-amp follows KCL. The output current is the sum of all input currents (the two inputs and V+, V-).
Where is the difference between the two inputs, and is the gain of the opamp:
Output voltage is limited by the maximum/minimum of the power supply .
If the output is fed directly into the inverting input (as a voltage follower), the gain is ignored and results in .
An ideal opamp has no input current and equal voltages entering the opamp.
Inverting amplifiers feed their input back and return negative voltage.
(Source: Wikimedia Commons)
Non-inverting amplifiers moves the voltage source to the non-inverting terminal.
(Source: Wikimedia Commons)
Voltage followers have either or , so:
(Source: Wikimedia Commons)
A summing amplifier splits an inverting amplifier's input into multiple voltage sources in series with resistances, all parallelised into the opamp:
(Source: Wikimedia Commons)
A difference amplifier is funky. To ensure that output is zero when inputs are equal, .
(Source: Wikimedia Commons)
Capacitors¶
Capacitors are open circuits in DC that store energy in electric fields. Capacitance is measured in farads ().
Where is the cross-section area of the wire, is the permittivity of the dielectric, and is the distance between plates:
Capacitors charge only when power is positive ().
For linear capacitors:
The energy in a capacitor can be interconverted.
Capacitor rules are the opposite of resistor rules.
- In parallel:
- In series:
Inductors¶
Inductors store energy in their magnetic field. Inductance is measured in henrys (). An ideal inductor has zero resistance and capacitance
Where is the inductance (opposition of charge flow):
Inductor rules are the same as resistor rules.
Selenoids¶
Selenoids have an inductance based on their cross sectional area , number of coils , length , and core permeability :
Where is the total current for
Much like capacitors, inductors have energy now based on current.
First-order circuits¶
Definition
- An RC circuit contains a resistor and a capacitor.
- An RL circuit contains a resistor and an inductor.
- First-order circuits contain derivatives.
- A source-free circuit assumes that energy already exists in the capacitor/inductor and no external energy enters the system.
- The circuit response is the behaviour of the circuit after excitation.
- The natural response is the behaviour of the circuit without external excitation.
The time constant is the time requirement for the circuit to decay to of its initial value. For RC circuits:
RL circuits have very similar formulae:
Singularity functions¶
The unit step function is a stair that is undefined at zero.
The unit impulse/delta function is the derivative of the unit step function.
The sudden spike at means that .
This function is related to signal strength. For the function , changing shifts the phase while shifting shifts amplitude.
To obtain at the impulse:
The unit ramp function is the integral of the unit step function.
Circuit responses¶
The total response to a circuit can be expressed as various combinations of:
- the natural response,
- the forced response (induced)
- the temporary response,
- the permanent/steady-state response,
In general, for current and voltage (), where is the final value and is the initial value:
A delayed response by shifts to and to .
Alternating current¶
Where is the amplitude of the voltage and is its angular frequency:
For a sinusoid's period , a circuit is period if and only if, for all :
Phasors¶
The phasor is the complex number vector version of the sinusoid in the time domain.
Please see MATH 115: Linear Algebra#Geometry for more information.
To transform time domains to frequency domains:
| Sinusoidal | Phasor |
|---|---|
The derivative of a phasor is itself multiplied by .
Adding sinusoids of the same frequency () is equivalent to adding their phasors.
If and are phasors:
- Inductors: ( lags by 90°)
- Capacitors: ( lags by 90°)
The scalar quantity of impedance represents the opposition to electron flow, measured in ohms.
It is effectively generalised resistance. Where is a positive value representing reactance such that implies inductance while implies capacitance:
Admittance is the inverse of impedance with units Siemens/mhos with factors conductance and susceptance:
Arranging equations yields
Steady state analysis¶
Kirchoff's laws only hold for phasor forms.
- Convert to phasor forms
- Solve phasor forms
- Convert back to time domain
Superposition must be summed at the end only, although individual components can first be solved.
- Convert to phasor forms
- Solve each individual current/voltage that make KCL/KVL
- Convert to time domain
- Apply KCL/KVL
When applying source transformations, different equivalent circuits for each frequency must be calculated individually — reducing it to one equivalent circuit is not possible.
Power¶
The average power is the integral average of instantaneous power:
Tip
The average of a sinusoid over its period is zero.
Alternatively, power can be calculated with magnitudes:
The same rules for maximum power transfer apply with resistance, but with as the complex conjugate of . The maximum power has a shortcut formula:
The effective value of a sinusoid is its DC equivalent. It is the root mean square.
The apparent power is the seemingly true power.
The power factor (pf) is the required factor to take the apparent power into real power.
The power factor angle is the angle of local impedance between voltage and current.
- A leading power factor has current lead voltage (capacitive)
- A lagging power factor has voltage lead current (inductive)
- A unity power factor has no phase shift
Complex power stores more phase information where .
These have units volt-amperes (VA).
The two components of complex power are actual power and reactive power , the latter with units VAR (volt-ampere reactive).
Complex power still follows most DC laws:
All powers (instantaneous, real, reactive, and complex) are conserved, except for apparent power.